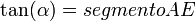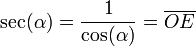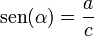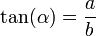El vampiro

Rey escapista

Lio en el bar

Circunferencia goniométrica 3

Por semejanza de triángulos: AE / AC = OA / OC
como OA = 1, se deduce que: AE = AC / OC

[editar] Razones trigonométricas recíprocas

La cosecante, la secante y la cotangente, son las razones trigonométricas recíprocas del seno, coseno y tangente:

Los valores de la cotangente, la secante y la cosecante se obtienen, análogamente, mediante semejanza de triángulos.

Topología

En topología, a la circunferencia unitaria (también denominado círculo unitario) se la clasifica como S¹; la generalización para una dimensión más es la esfera unidad S².

Circunferencia goniométrica 2

Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:
El seno es la razón entre el cateto opuesto (a) y la hipotenusa (c)

y dado que la hipotenusa es igual al radio, que tiene valor = 1, se deduce:

El coseno es la razón entre el cateto adyacente (b) y la hipotenusa (c)

y como la hipotenusa tiene valor = 1, se deduce:

La tangente es la razón entre el cateto opuesto y el adyacente

Circunferencia goniométrica 1

La circunferencia goniométrica, trigonométrica, unitaria o «círculo unidad» es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación: